
指数と対数
電波の測定値は、場所や時間などの環境によって、何桁も違う数値となることがあります。そのような場合、指数や対数を使うと数値を扱いやすくなります。ここでは、指数や対数の解説と、対数を使う単位について解説します。
指数・対数とは
指数
ある数を別の数の何乗で表せるかで示すとき、「指数」を使います。例えば、
10000 = 104 (10000は10の4乗)
0.001 = =10-3 (0.001は10のマイナス3乗)
のように表現します。一般的には、以下の式のように書くことができます。
A = NB (AはNのB乗)
このとき、Aを真数、Bを指数と呼びます。指数は上付きの文字として表記します。最初の2つの例はN=10の場合ですが、Nは他の数でも構いません。また、2つ目の例のように指数が負の数の場合は、その絶対値を指数とした数の逆数となります。
対数
一方、指数を求めるときには、「対数」を用います。対数の表記には「log(ログ)」という記号を使います。上記の式は、対数を使うと以下のように書き換えることができます。
= B (真数AのNを底とする対数はB)
ここで、log記号の後に下付き文字で書く数値Nを「底(てい)」と言います。底を10とする対数は、常用対数とも呼ばれます。したがって、真数Aに対する常用対数Bは、以下の式のように書くことができます。
= B (真数Aの10を底とする対数(常用対数)はB)
これを上記の指数の項で示した例にあてはめると、以下のように書き換えることができます。
=4 (10000の10を底とする対数は4)
=-3 (0.001の10を底とする対数は-3)
また、10の累乗ではない数も対数で表現することができます。例えば、1から10までの数の対数(B)は以下の表のようになります。
| 真数(A) | 常用対数(B) | 指数を用いた式 | 対数を用いた式 |
|---|---|---|---|
| 1 | 0 | 1 = 100 | =0 |
| 2 | 0.301 | 2 = 100.301 | =0.301 |
| 3 | 0.477 | 3 = 100.477 | =0.477 |
| 4 | 0.602 | 4 = 100.602 | =0.602 |
| 5 | 0.699 | 5 = 100.699 | =0.699 |
| 6 | 0.778 | 6 = 100.778 | =0.778 |
| 7 | 0.845 | 7 = 100.845 | =0.845 |
| 8 | 0.903 | 8 = 100.903 | =0.903 |
| 9 | 0.954 | 9 = 100.954 | =0.954 |
| 10 | 1 | 10 = 101 | =1 |
対数で表す単位
デシベル(dB)とは
デシベル(dB; 「デービー」とも読みます)は、2つの数値の比を対数を用いて表現する際に用いられ、数値がどれだけ大きいか(あるいは小さいか)を示すことができます。対数を使うことにより、何桁にもわたるような広い範囲の数値を扱いやすく表現できることが特徴です。騒音レベルや地震の規模(マグニチュード)、電力、電圧など、いろいろな場面で利用されています。
例えば、電力の場合、基準となる値 (W) に対して別の値(例えば測定値)を (W) としたとき、両者の比 (dB) は以下のように計算できます。
電圧の場合は、基準となる値 (V) に対して別の値(例えば測定値)を (V) としたとき、両者の比 (dB) は以下のように計算できます。
例えば電力の値が1~1010に分布している場合、下図のように値の分布を見るためにヒストグラムを描くときに真数よりも対数(dB)を横軸に取って描いた方が分布を捉えやすいことがわかります。
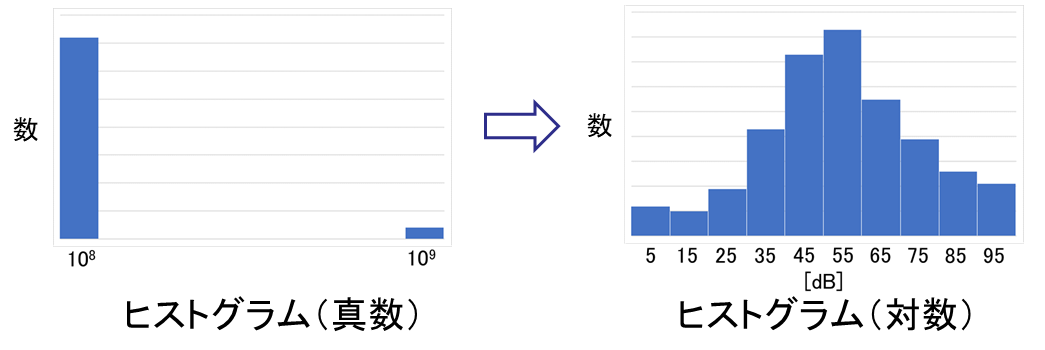
(左)真数を横軸に取るヒストグラム (右)対数(dB)を横軸に取るヒストグラム
デシベルを用いた単位
基準となる値との比率として記述することにより、デシベルは様々な物理量の単位にも利用されます。例えば、電波レベル(電界強度)の場合は、dBµV/m (デシベルマイクロボルト毎メートル、もしくはデービーマイクロボルト毎メートル)という単位がよく使われます。これは、1 (µV/m) を 0 (dBµV/m) とする、つまり
と定義し、これを基準とした相対値として表現する単位です。
例えば、測定された電界強度の真数での値を (µV/m) とすると、そのデシベルを用いた単位での表現 は、次式から計算することができます。
代表的な値を計算してみると、以下の表のようになります。真数の値が10倍大きくなる毎に 20 (dBµV/m) 増える関係になることがわかります。したがって、1000000(百万)倍違う値がデシベルを用いると0から120 (dBµV/m) までの範囲に収まることになります。本サイト内の電測車による電界強度の測定についてに掲載しているグラフではこの単位を使用しています。
| E1 | E (dBµV/m) |
|---|---|
| 0.000001 (V/m) = 1 (µV/m) | 0 (dBµV/m) |
| 0.00001 (V/m) = 10 (µV/m) | 20 (dBµV/m) |
| 0.0001 (V/m) = 100 (µV/m) | 40 (dBµV/m) |
| 0.001 (V/m) = 1000 (µV/m) | 60 (dBµV/m) |
| 0.01 (V/m) = 10000 (µV/m) | 80 (dBµV/m) |
| 0.1 (V/m) = 100000 (µV/m) | 100 (dBµV/m) |
| 1 (V/m) = 1000000 (µV/m) | 120 (dBµV/m) |
